CoqIDE
Nous utiliserons CoqIDE (commandecoqide
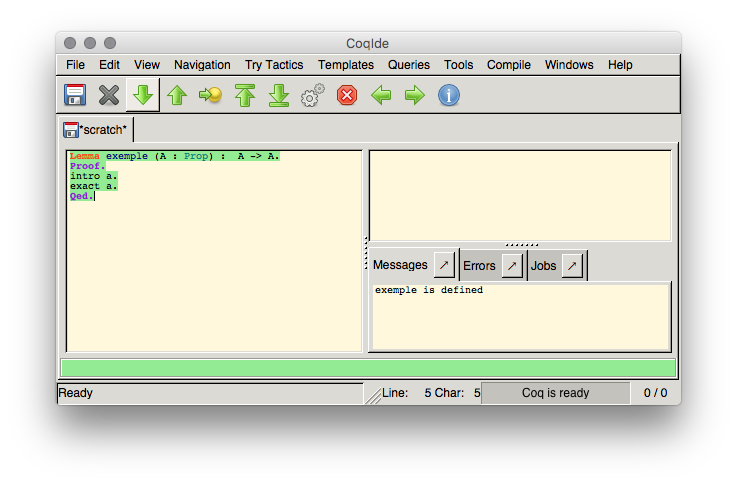
). La fenêtre de coq possède 3 zones : la zone d'entrée où vous tapez votre programme à gauche, la zone affichant l'état courant de la preuve en haut à droite, et la zone des messages en bas à droite.Dans l'exemple ci-dessous nous définissons un lemme commé exemple, dépendant d'une proposition
A
, et défini comme A -> A
(A implique A). La preuve est notée entre Proof
(preuve) et Qed
(Quod Erat Demonstratum : CQFD en latin). Vous pouvez copier-coller ce texte :
Lemma exemple (A : Prop) : A -> A.
Proof.
intro a.
exact a.
Qed.
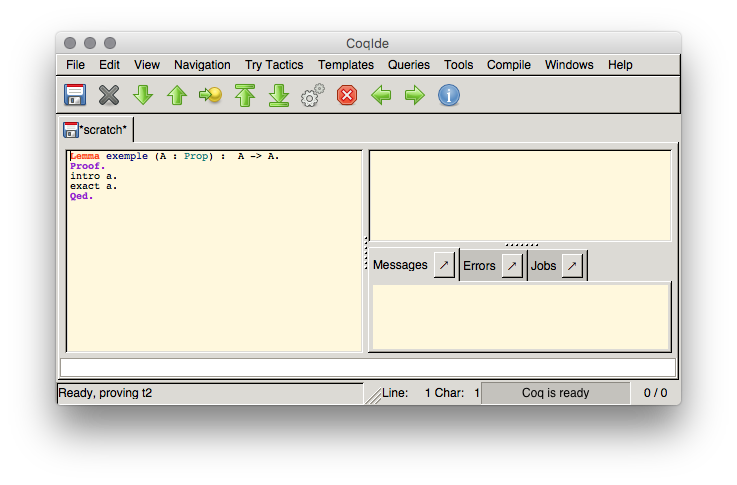 Remarquez les flèches dans la barre de menu. Elles vont vous servir à naviguer dans votre programme. La flèche vers le bas permet d'avancer d'une ligne. La flèche vers le haut recule d'une ligne. La flèche à droite avance (ou recule) jusqu'au curseur, et les deux dernières vont soit tout au début soit tout à la fin. La partie vérifiée est surlignée en vert comme ci-dessous. En cas d'erreur le surlignage est rouge, et on ne peut pas progresser tant que l'erreur n'est pas corrigée. Il faut parfois remonter dans la preuve car il est possible que le raisonnement validé jusque là ne permet pas d'aboutir.
Remarquez les flèches dans la barre de menu. Elles vont vous servir à naviguer dans votre programme. La flèche vers le bas permet d'avancer d'une ligne. La flèche vers le haut recule d'une ligne. La flèche à droite avance (ou recule) jusqu'au curseur, et les deux dernières vont soit tout au début soit tout à la fin. La partie vérifiée est surlignée en vert comme ci-dessous. En cas d'erreur le surlignage est rouge, et on ne peut pas progresser tant que l'erreur n'est pas corrigée. Il faut parfois remonter dans la preuve car il est possible que le raisonnement validé jusque là ne permet pas d'aboutir.Après avoir avancé d'une ligne, observez l'état courant en haut à droite. Coq vous dit qu'il y a une preuve à faire (
1 subgoal
), que parmi nos hypothèses A est une proposition et qu'il faut montrer A -> A
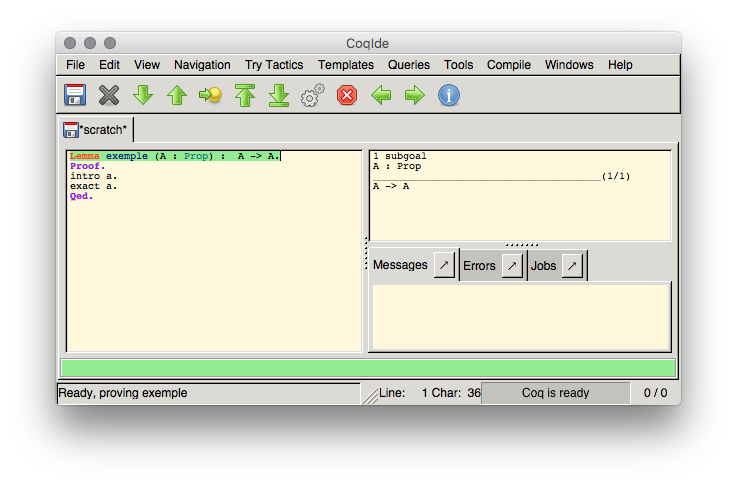 Pour prouver
Pour prouver A -> A
nous voulons faire un « implique intro », comme en déduction naturelle. Nous utilisons la tactique intro
, qui nous permet d'introduire le A
de gauche parmi nos hypothèses, et de nommer ce A
(a
). E avançant dans la preuve on observe que parmi nos hypothèses nos disposons de a
qui est une preuve de A
, et qu'il faut montrer A
.
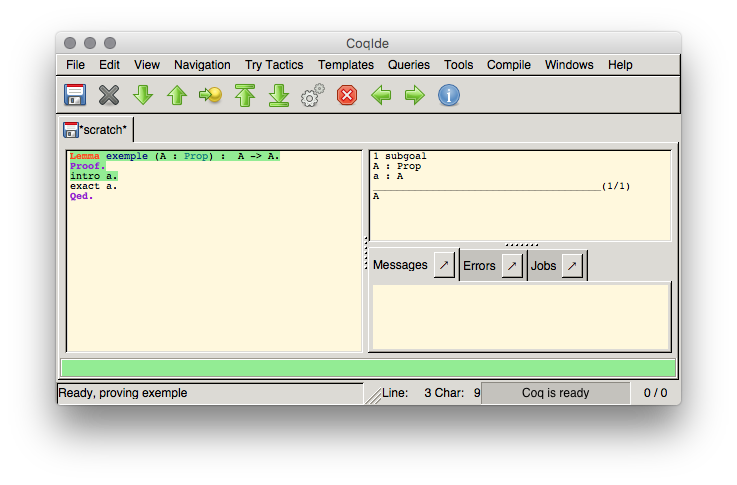 Cette preuve est facile (pour ne pas dire triviale) car nous disposons d'une preuve de ce que l'on doit prouver. Cette preuve a un nom :
Cette preuve est facile (pour ne pas dire triviale) car nous disposons d'une preuve de ce que l'on doit prouver. Cette preuve a un nom : a
. Nous utilisons la tactique exact
, qui permet de terminer la preuve. Coq nous dit que la preuve est terminée : « No more subgoals ».
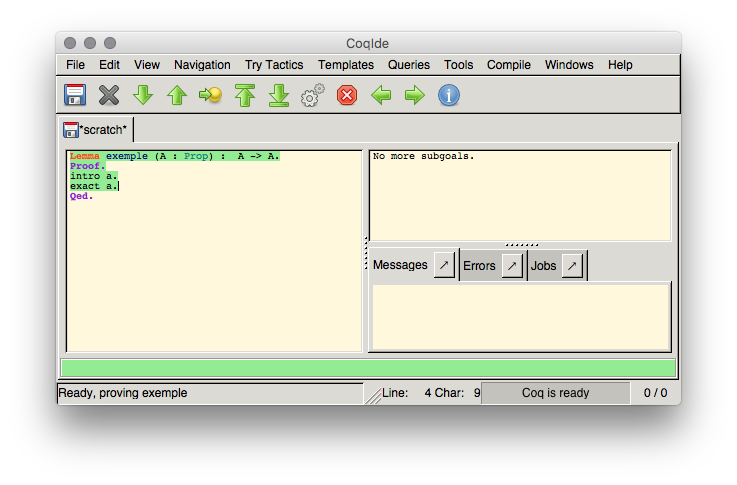 Après avoir avancé après
Après avoir avancé après Qed.
, Coq nous dit que notre lemme est défini. Nous pouvons désormais l'utiliser avec la tactique apply
.
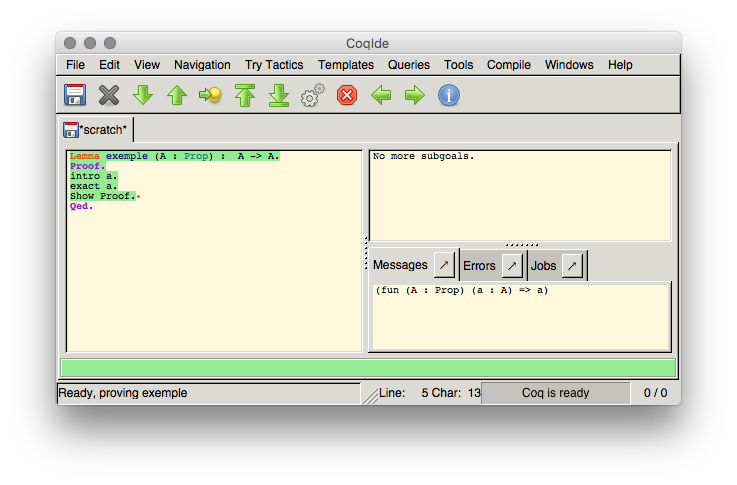
 À toute preuve de Coq correspond un programme. Nous pouvons à tout moment afficher ce programme avec la commande
À toute preuve de Coq correspond un programme. Nous pouvons à tout moment afficher ce programme avec la commande Show Proof
. Dans notre example, ce programme est une fonction prenant en paramètre un « type de proposition » nommé A
et un objet a
de ce type, et renvoie cet objet en résultat.
Tactiques
Les preuves dans Coq sont réalisées à l'aide de tactiques. Ces tactiques permettent de manipuler le but (la preuve à réaliser) et les hypothèses. Elles sont similaires aux preuves en déduction naturelle, sauf que certaines règles utilisent la même tactique. Dans ce TP vous n'aurez le droit qu'à ces tactiques. Il existe d'autres tactiques plus puissantes, mais qui gâchent l'intérêt pédagogique dans le cadre de ce TP.| Connecteur | Introduction | Elimination |
|---|---|---|
| Implique -> | intro | apply |
| Non ~ | intro | apply |
| Et /\ | split | destruct _ as [_ _] |
| Ou \/ | left right | destruct _ as [_|_] |
| Equivalence <-> | split | apply apply <- |
| Pour tout forall | intro | apply |
| Il existe exists | exists | destruct as [_ _] |
| Egalité = | reflexivity | rewrite rewrite <- |
| Bottom e | destruct |
intro
possède une variante intros
permettant d'introduire plusieurs hypothèses.
Partie 1
Démontrez les lemmes suivants :Lemma hilbertS (A B C : Prop) : (A -> B -> C) -> (A -> B) -> A -> C.
Lemma q2 (A B : Prop) : A -> (B -> A).
Lemma q3 (A B : Prop) : A -> (~A -> B).
Lemma q4 (A B C : Prop) : (A -> B) -> ((B -> C) -> (A -> C)).
Lemma q5 (A B : Prop) : (A -> B) -> (~B -> ~A).
A \/ ~A
), la double négation (A -> ~~A
) ou le raisonnement par l'absurde ((~A -> False) -> A
). Pour cela nous allons charger la librairie Classical
:
Require Import Classical.
Vous pourrez ainsi utiliser la nouble négation avec la commande apply NNPP.
.
Lemma tiersexclus (A : Prop) : A \/ ~A.
Lemma bottom_c (A : Prop) : (~A -> False) -> A.
Lemma q8 (A B : Prop) : (~B -> ~A) -> (A -> B).
+
, *
, -
.
Lemma q9 (A : Prop) : ~~A <-> A.
Lemma q10 (A : Prop) : (A /\ ~A) <-> False.
Lemma q11 (A B : Prop) : (A \/ B) <-> ~(~A /\ ~B).
Lemma q12 (A : Prop) : ~A <-> (A -> False).
Lemma q13 (A B : Prop) : (A <-> B) <-> (A -> B) /\ (B -> A).
Lemma q14 (A B C : Prop) : (A /\ B -> C) <-> (A -> B -> C).
Lemma q15 (A B C : Prop) : (C -> A)\/ (C -> B) <-> (C -> A \/ B).
Lemma q16 (X : Type) (A B : X -> Prop) :
((forall x, A x) \/ (forall x, B x)) -> forall x, A x \/ B x.
Lemma q17 (X : Type) (A B : X -> Prop) :
(exists x, A x /\ B x) -> ((exists x, A x) /\ (exists x, B x)).
Lemma q18 (A B : Prop) : ~ (A /\ B) -> (~ A \/ ~ B).
Lemma q19 (X : Type) : forall (x1 x2 : X), x1 = x2 -> x2 = x1.
Lemma q20 (X : Type) : forall (x1 x2 x3 : X), x1 = x2 /\ x2 = x3 -> x1 = x3.
Partie 2
Nous avons utilisé jusque là les connecteurs de Coq, qui sont basés sur les types inductifs. Nous allons maintenant définir les connecteurs avec le quantificateur universel (pour tout) et l'implication et prouver les règles de déduction.Definition faux := forall (P : Prop), P.
Definition non (A : Prop) :=
forall (P : Prop), ((A -> faux) -> P) -> P.
Definition et (A B : Prop) :=
forall (P : Prop), (A -> B -> P) -> P.
Definition ou (A B : Prop) :=
forall (P : Prop), ((A -> P) -> (B -> P) -> P).
Definition existe (A : Type) (P : A -> Prop) :=
forall (Q : Prop), (forall a, P a -> Q) -> Q.
Definition egal (A : Type) (a a' : A) :=
forall (P : A -> Prop), P a -> P a'.
Montrez la règle bottom e:
Lemma bottom_e (A : Prop) : faux -> A.
Montrez les règles de l'opérateur non :
Lemma non_intro (A : Prop) : (A -> faux) -> non A.
Lemma non_elim (A : Prop) : A -> non A -> faux.
Montrez les règles de l'opérateur et :
Lemma et_intro (A B : Prop) : A -> B -> et A B.
Lemma et_elim_g (A B : Prop) : et A B -> A.
Lemma et_elim_d (A B : Prop) : et A B -> B.
Montrez les règles de l'opérateur ou :
Lemma ou_intro_g (A B : Prop) : A -> ou A B.
Lemma ou_intro_d (A B : Prop) : B -> ou A B.
Lemma ou_elim (A B C : Prop) : ou A B -> (A -> C) -> (B -> C) -> C.
Montrez les règles de l'opérateur existentiel :
Nous pouvons aussi vérifier que les connecteurs que nous avons définis sont équivalents à ceux de Coq :
Lemma existe_intro (A : Type) (P : A -> Prop) : forall x : A, P x -> existe A P.
Lemma existe_elim (A : Type) (P : A -> Prop) (Q : Prop) :
existe A P -> (forall x : A, P x -> Q) -> Q.
Lemma faux_false : faux <-> False.
Lemma non_not (A : Prop) : non A <-> ~A.
Lemma et_and (A B : Prop) : et A B <-> A /\ B.
Lemma ou_or (A B : Prop) : ou A B <-> A \/ B.
Lemma existe_exists (A : Type) (P : A -> Prop) : existe A P <-> exists a, P a.
Lemma egal_eq (A : Type) (a a' : A) : egal _ a a' <-> a = a'.